Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Приобрести бетон М300 с доставкой в компании ООО "БСК".
|
Линейные пространства и линейные отображения / Жорданова нормальная форма / 1 2 3 4 5 6 7 8 9 10
Покажем, что вид циклической клетки, отвечающей f, не зависит от выбора исходного циклического вектора. Для этого проверим, что первый столбец клетки состоит из коэффициентов минимального многочлена оператора В самом деле, M(f) = 0, потому что M(f)[fi(l)] = fi[M(f)l] = 0, а векторы fi(l) порождают L. С другой стороны, если N(t) - многочлен степени < n, то б) Критерий цикличности пространства. Согласно предыдущим рассмотрениям, если пространство L циклично относительно f, то его размерность n равна степени минимального многочлена оператора f и, стало быть, минимальный многочлен совпадает с характеристическим. Обратное тоже верно: если операторы id, f, ..., fn-1 линейно независимы, то существует такой вектор l, что векторы l, f(l), ..., fn-1(l) линейно независимы, так что L циклично. Мы не будем доказывать это утверждение. в) Матрица любого оператора в подходящем базисе может быть приведена к прямой сумме циклических клеток. Доказательство можно провести аналогично доказательству теоремы о жордановой форме. Вместо множителей |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
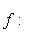
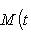
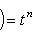
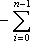
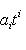 .
.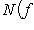
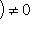 , потому что иначе, применив оператор N(f) = 0 к циклическому вектору l, получим нетривиальное линейное соотношение между векторами базиса l, f(l), ..., fn-1(l).
, потому что иначе, применив оператор N(f) = 0 к циклическому вектору l, получим нетривиальное линейное соотношение между векторами базиса l, f(l), ..., fn-1(l).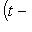
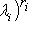 характеристического многочлена следует рассматривать множители
характеристического многочлена следует рассматривать множители 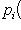
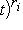 , где pi(t) - неприводимые над полем
, где pi(t) - неприводимые над полем