Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Доставка цветов в Кош-Агаче: купить подставки для цветов среди-цветов.ру. ; https://gos-ritual.ru ритуальный агент стоимость услуг низкие цены.
Линейные пространства и линейные отображения / Жорданова нормальная форма / 1 2 3 4 5 6 7 8 9 10
Жорданова нормальная форма1. Теорема о существовании и единственности жордановой нормальной формы для матриц и линейных операторов. а) Для оператора f существует жорданов базис, т. е. его матрица A в некотором базисе может быть приведена заменой базиса X к жордановой форме: X -1AX = J. б) Матрица J определена однозначно с точностью до перестановки входящих в нее жордановых клеток. 2. Доказательство теоремы разбивается на ряд промежуточных шагов. Начнем с конструкции прямого разложения 3. Определение. Вектор Очевидно, все собственные векторы корневые. 4. Предложение. Обозначим через |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
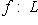
 - линейный оператор. Тогда:
- линейный оператор. Тогда: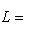
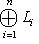 , где Li - инвариантные подпространства для f, которые впоследствии будут отвечать набору жордановых клеток для f с одним и тем же числом
, где Li - инвариантные подпространства для f, которые впоследствии будут отвечать набору жордановых клеток для f с одним и тем же числом 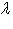 на диагонали. Чтобы инвариантно охарактеризовать эти подпространства, вспомним, что
на диагонали. Чтобы инвариантно охарактеризовать эти подпространства, вспомним, что 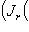
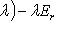
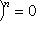 . Оператор, некоторая степень которого равна нулю, принято называть нильпотентным. Итак, на подпространстве, отвечающем клетке
. Оператор, некоторая степень которого равна нулю, принято называть нильпотентным. Итак, на подпространстве, отвечающем клетке 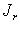
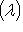 , оператор
, оператор 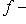
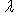 нильпотентен; то же верно для его ограничения на сумму подпространств с фиксированным
нильпотентен; то же верно для его ограничения на сумму подпространств с фиксированным 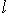
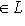 называется корневым вектором оператора f, отвечающим
называется корневым вектором оператора f, отвечающим 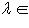
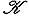 , если существует такое r, что
, если существует такое r, что 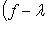
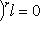 (здесь
(здесь 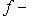
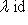 ).
).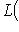
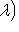 множество корневых векторов оператора f в L, отвечающих
множество корневых векторов оператора f в L, отвечающих 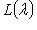
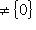 тогда и только тогда, когда
тогда и только тогда, когда