Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Геометрия пространств со скалярным произведением / Ортогональные и унитарные операторы / 1 2 3 4 5 6 7
Ортогональные и унитарные операторы1. Пусть L - линейное пространство со скалярным произведением g. Множество всех изометрий g(f(l1), f(l2)) = g(l1, l2) для всех 2. Предложение. Пусть L - конечномерное линейное пространство с невырожденным скалярным произведением ( , ), симметричным или эрмитовым. Для того чтобы оператор а) (f(l), f(l)) = (l, l) для всех б) пусть {e1, ..., en} - базис в L с матрицей Грама G, A - матрица оператора f в этом базисе. Тогда
в) f переводит некоторый ортонормированный базис в ортонормированный базис; |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

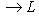 , т. е. обратимых линейных операторов с условием
, т. е. обратимых линейных операторов с условием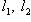
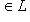 , очевидно, образует группу. Если L - евклидово пространство, такие операторы называются ортогональными, а если L унитарно, то унитарными. Симплектические изометрии будут рассмотрены позже.
, очевидно, образует группу. Если L - евклидово пространство, такие операторы называются ортогональными, а если L унитарно, то унитарными. Симплектические изометрии будут рассмотрены позже.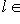
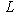 (здесь предполагается, что характеристика поля скаляров отлична от двух);
(здесь предполагается, что характеристика поля скаляров отлична от двух);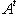
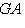
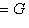 , или
, или 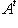
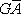
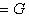 ;
;