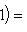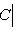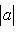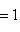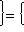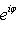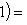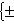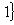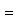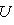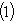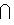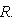Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Ортогональные и унитарные операторы / 1 2 3 4 5 6 7
б) Если f-изометрия, то матрицы Грама базисов {e1, ..., en} и {f(e1), ..., f(en)} совпадают. Но последняя матрица Грама равна AtGA в симметричном и в), г). Эти утверждения являются частными случаями предыдущих. Из предложения п. 2 следует, что ортогональные (соответственно унитарные) операторы - это операторы, которые в одном (и потому в любом) ортонормированном базисе задаются ортогональными (соответственно унитарными) матрицами, т. е. матрицами U, которые удовлетворяют соотношениям
Множества таких матриц размера 3. Группы U(1), O(1) и O(2). Из определения немедленно следует, что
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
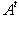
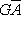 в эрмитовом случае. Наоборот, если f переводит базис {e1, ..., en} в
в эрмитовом случае. Наоборот, если f переводит базис {e1, ..., en} в 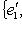
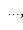
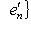 и матрицы Грама базисов {ei} и
и матрицы Грама базисов {ei} и 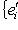
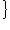 совпадают, то f-изометрия в силу формул координатной записи скалярного произведения из
совпадают, то f-изометрия в силу формул координатной записи скалярного произведения из 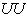
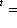
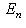 или
или 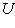
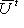
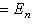 .
.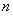
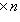 были введены впервые в разделе
были введены впервые в разделе 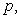
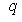
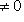 они называются иногда псевдоортогональными и псевдоунитарными соответственно. В этом разделе мы будем заниматься только группами O(n) и U(n). Фундаментальная для физики группа Лоренца O(1, 3) будет рассмотрена в разделе
они называются иногда псевдоортогональными и псевдоунитарными соответственно. В этом разделе мы будем заниматься только группами O(n) и U(n). Фундаментальная для физики группа Лоренца O(1, 3) будет рассмотрена в разделе