Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Линейные пространства и линейные отображения / Факторпространства / 1 2 3 4 5 6
Факторпространства1. Пусть L - линейное пространство,
"сдвигов" линейного пространства M на вектор l. Вскоре мы убедимся, что такие сдвиги не обязаны быть линейными подпространствами в L; их называют линейными подмногообразиями. Начнем с доказательства следующей леммы. 2. Лемма. l1 + M1 = l2 + M2 тогда и только тогда, когда M1 = M2 = M и Доказательство. Прежде всего, пусть
Но когда m пробегает все векторы из M, m - m0 тоже пробегает все векторы из M. Поэтому l1 + M = l2 + M. Наоборот, пусть l1 + M1 = l2 + M2. Положим m0 = l1 + l2. Из определения ясно, что тогда m0 + M1 = M2. Так как |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
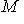
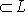 - его линейное подпространство, а
- его линейное подпространство, а 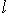
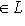 - вектор. Различные вопросы приводят к рассмотрению множеств вида
- вектор. Различные вопросы приводят к рассмотрению множеств вида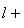
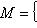
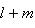
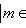
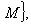
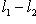
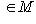 . Таким образом, всякое линейное подмногообразие однозначно определяет линейное подпространство M, сдвигом которого оно является. Вектор же сдвига определяется лишь с точностью до элемента из этого подпространства.
. Таким образом, всякое линейное подмногообразие однозначно определяет линейное подпространство M, сдвигом которого оно является. Вектор же сдвига определяется лишь с точностью до элемента из этого подпространства.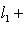
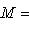
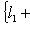
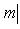
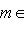
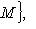
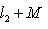
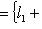
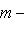
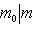
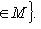
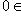
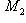 , мы должны иметь
, мы должны иметь 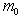
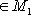 . Значит, m0 + M1 = M1 по рассуждению в предыдущем абзаце, так что M1 = M2 = M. Это завершает доказательство.
. Значит, m0 + M1 = M1 по рассуждению в предыдущем абзаце, так что M1 = M2 = M. Это завершает доказательство.