Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Структура линейного отображения / 1 2 3 4 5 6 7 8 9 10
Пример такой матрицы: Далее покажем, что именно такие матрицы образуют "строительные блоки" для нормальной формы общего линейного оператора над алгебраически замкнутым полем. Дадим общее определение: 9. Определение. а) Жордановой клеткой
б) Жордановой матрицей называется матрица, состоящая из диагональных блоков
в) Жордановым базисом для оператора г) Приведением квадратной матрицы A к жордановой нормальной форме называется решение уравнения в матрицах вида X -1AX = J, где X - (неизвестная) невырожденная матрица, а J - (неизвестная) жорданова матрица. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
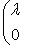
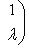 . Эта матрица называется жордановой клеткой размера
. Эта матрица называется жордановой клеткой размера 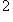
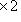 (или ранга 2).
(или ранга 2).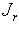
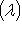 размера
размера 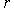
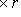 с собственным значением
с собственным значением 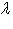 называется матрица вида
называется матрица вида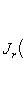
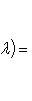
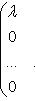
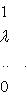

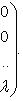
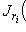
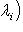 и нулей вне этих блоков:
и нулей вне этих блоков: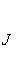
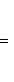
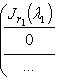
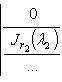

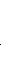
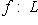
 называется такой базис пространства L, в котором матрица оператора f является жордановой, или, как говорят, имеет жорданову нормальную форму.
называется такой базис пространства L, в котором матрица оператора f является жордановой, или, как говорят, имеет жорданову нормальную форму.