Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Структура линейного отображения / 1 2 3 4 5 6 7 8 9 10
Согласно определению п. 3, диагонализируемые операторы f допускают разложение L в прямую сумму своих собственных подпространств. Выясним, когда у f имеется хотя бы одно собственное подпространство. 5. Определение. Пусть L - конечномерное линейное пространство, 6. Теорема. а) Характеристический многочлен линейного оператора f не зависит от выбора базиса, в котором представлена его матрица. б) Любое собственное значение оператора является корнем P(t) и любой корень P(t), лежащий в Доказательство. а) Согласно п. 7 матрица оператора f в другом базисе имеет вид B-1AB. Поэтому, пользуясь мультипликативностью определителя, находим det(tE - B -1AB) = det(B -1(tE - A)B) = = (det B) -1det(tE - A)det B = det(tE - A). Заметим, что |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
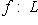
 - линейный оператор, A - его матрица в каком-нибудь базисе. Обозначим через P(t) и назовем характеристическим многочленом оператора f, а также матрицы A, многочлен det(tE - A) с коэффициентами в поле
- линейный оператор, A - его матрица в каком-нибудь базисе. Обозначим через P(t) и назовем характеристическим многочленом оператора f, а также матрицы A, многочлен det(tE - A) с коэффициентами в поле 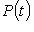
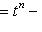
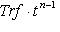
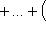
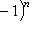
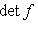 (обозначения из
(обозначения из