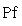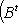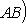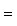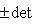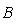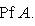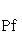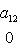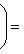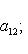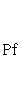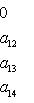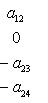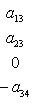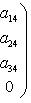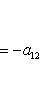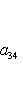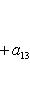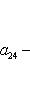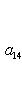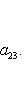Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Симплектические пространства / 1 2 3 4 5 6 7 8
Последнее равенство из формулировки теоремы устанавливается так. Прежде всего, BtAB кососимметрична вместе с A, так что Pf2(BtAB) = det(BtAB) = (det B)2det A = (det B)2Pf2A. Поэтому
Чтобы установить знак, достаточно выяснить его в случае A = I2r, B = E2r, где он, очевидно, положителен. 10. Примеры.
11. Следствие. Определитель любой симплектической матрицы равен единице. Доказательство. Из условия AtI2rA = I2r и теоремы п. 9 следует 1 = Pf I2r = Pf(AtI2rA) = det A Pf I2r, что доказывает требуемое. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник