Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Подпространства и прямые суммы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Прежде всего, Матрицы Результатом деформации A на этом этапе будет матрица композиции двух преобразований: одно сводится к перестановке векторов базиса (Fs, t меняет местами s-й и t-й вектор), другое меняет знаки части векторов (композиция Fs(+1) и Ft(-1)). Любую перестановку можно разложить в произведение попарных перестановок. Матрицу перестановки векторов базиса в плоскости К этому моменту A превратилась в диагональную матрицу с элементами Вернемся теперь к ориентации. -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
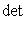
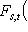
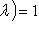 при всех
при всех 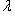 и Fs, t(0) = E. Меняя в исходных сомножителях
и Fs, t(0) = E. Меняя в исходных сомножителях 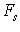
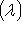 диагональны: на месте (s, s) стоит
диагональны: на месте (s, s) стоит 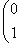
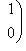 можно соединить с
можно соединить с 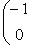
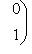 кривой
кривой 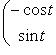
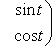 ,
, 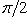
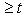
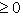 . Очевидно, разнеся элементы последней матрицы по местам (s, s), (s, t), (t, s), (t, t), получим соответствующую деформацию в любой размерности, уничтожающую множители Fs, t.
. Очевидно, разнеся элементы последней матрицы по местам (s, s), (s, t), (t, s), (t, t), получим соответствующую деформацию в любой размерности, уничтожающую множители Fs, t.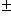
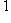 на диагонали, причем число минус единиц четно, т. к. определитель A положителен. Матрицу
на диагонали, причем число минус единиц четно, т. к. определитель A положителен. Матрицу 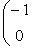
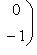 можно соединить с
можно соединить с 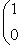
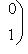 кривой
кривой 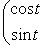
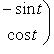 ,
, 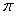
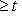
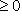 . Собрав все -1 попарно и проведя такие деформации всех пар, мы завершим доказательство.
. Собрав все -1 попарно и проведя такие деформации всех пар, мы завершим доказательство.