Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Подпространства и прямые суммы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
12. Внешние прямые суммы. Пусть теперь L1, ..., Ln - пространства, не вложенные заранее в общее пространство. Определим их внешнюю прямую сумму L следующим образом: а) L как множество есть б) Сложение и умножение на скаляр производятся покоординатно:
Нетрудно проверить, что L удовлетворяет аксиомам линейного пространства. Отображение 13. Прямые суммы линейных отображений. Пусть -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
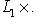
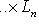 , т. е. элементы L суть семейства (l1, ..., ln), где
, т. е. элементы L суть семейства (l1, ..., ln), где 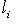
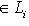 .
.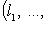
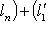
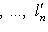
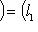
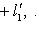
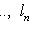
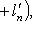
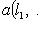
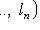
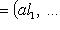
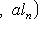
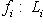
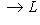 , fi(l) = (0, ..., 0, l, 0, ..., 0) (l на i-м месте) является линейным вложением Li в L, и из определений немедленно следует, что
, fi(l) = (0, ..., 0, l, 0, ..., 0) (l на i-м месте) является линейным вложением Li в L, и из определений немедленно следует, что 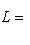
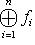
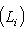 . Отождествив Li с fi(Li), получим линейное пространство, в котором Li содержатся и которое разлагается в прямую сумму Li. Это оправдывает название внешней прямой суммы. Часто удобно обозначать внешнюю прямую сумму также
. Отождествив Li с fi(Li), получим линейное пространство, в котором Li содержатся и которое разлагается в прямую сумму Li. Это оправдывает название внешней прямой суммы. Часто удобно обозначать внешнюю прямую сумму также 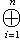
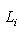 .
.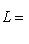
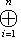
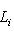 ,
, 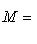
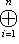
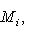
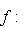
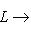
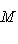 - такое линейное отображение, что
- такое линейное отображение, что 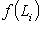
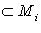 . Обозначим через fi индуцированное линейное отображение
. Обозначим через fi индуцированное линейное отображение 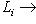
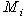 . В таком случае принято писать
. В таком случае принято писать 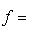
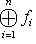 . Аналогично определяется внешняя прямая сумма линейных отображений. Выбрав в L и M базисы, являющиеся объединением базисов Li и Mi соответственно, мы получаем, что матрица f является объединением стоящих по диагонали блоков, которые представляют собой матрицы отображений fi; на остальных местах стоят нули.
. Аналогично определяется внешняя прямая сумма линейных отображений. Выбрав в L и M базисы, являющиеся объединением базисов Li и Mi соответственно, мы получаем, что матрица f является объединением стоящих по диагонали блоков, которые представляют собой матрицы отображений fi; на остальных местах стоят нули.