Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Геометрия квадратичных форм и собственные значения самосопряженных операторов / 1 2 3 4 5 6 7 8 9 10 11
8. Предложение. Пусть
Доказательство. Поскольку
На единичной сфере левая часть есть 9. Следствие. Пусть
Доказательство. Действительно, в очевидных координатах ограничение qf на Следующее важное усиление этого результата, в котором вместо |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
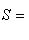
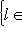
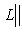
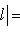
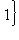 - единичная сфера пространства L. Тогда
- единичная сфера пространства L. Тогда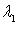
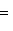
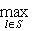
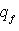
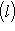
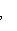
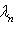
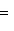
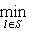
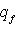
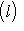
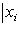
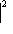
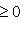 и
и 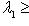
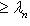 , очевидно
, очевидно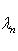
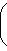
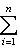
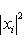
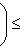
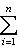
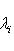
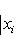
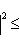
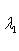
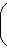
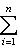
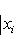

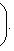
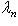 , а правая
, а правая 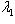 . Эти значения достигаются на векторах (0, ..., 0, 1) и (1, 0, ..., 0) соответственно (координаты берутся в базисе {e1, ..., en}, диагонализирующем f).
. Эти значения достигаются на векторах (0, ..., 0, 1) и (1, 0, ..., 0) соответственно (координаты берутся в базисе {e1, ..., en}, диагонализирующем f).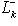 - линейная оболочка семейства {e1, ..., ek},
- линейная оболочка семейства {e1, ..., ek}, 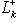 - линейная оболочка семейства {ek, ..., en}. Тогда
- линейная оболочка семейства {ek, ..., en}. Тогда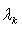
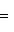
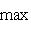
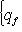
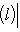
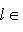
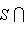
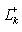
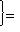
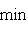
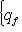
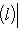
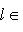
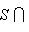
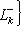
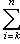
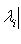
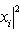 , а ограничение на
, а ограничение на 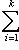
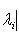
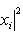 .
.