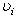
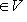6. Теория Морса. Представим себе в (n + 1)-мерном евклидовом пространстве Rⁿ⁺¹ n-мерную гладкую ограниченную гиперповерхность V, вроде яйца или баранки (тора) в R³. Рассмотрим сечения V гиперплоскостями x_n+1 = const. Предположим, что имеется только конечное число значений c₁, ..., c_m таких, что гиперплоскости x_n+1 = c_i касаются V и притом в единственной точке . 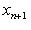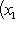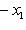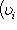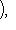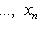Вблизи этих точек касания V можно приблизить графиком квадратичной формы 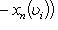, если только V находится в достаточно общем положении (например, бублик не должен лежать горизонтально). Оказывается, что важнейшие топологические свойства V, - в частности, так называемый гомотопический тип V - вполне определяются набором сигнатур форм q_i, т. е. указанием того, по скольким направлениям V вблизи 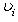уходит вниз и по скольким - вверх. Самое замечательное то, что, хотя информация о сигнатурах q_i чисто локальна, восстанавливаемый по ней гомотопический тип V есть глобальная характеристика формы V. Например, если имеются только две критические точки c₁ и c₂ с сигнатурами (n, 0) и (0, n), то V топологически устроена как n-мерная сфера.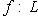

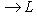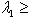
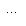
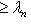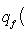
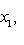
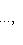
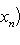
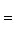
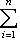
7. Самосопряженные операторы и многомерные квадрики. Пусть теперь L - конечномерное евклидово или унитарное пространство, - самосопряженный оператор. Нас интересуют свойства его спектра. Расположим собственные значения f в порядке убывания с учетом кратностей: и выберем соответствующий ортонормированный базис {e₁, e₂, ..., e_n}. Вернемся к точке зрения 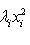п. 4, согласно которой задание f равносильно заданию новой симметричной или эрмитовой формы (f(l₁), l₂) или же квадратичной формы q_f(l) = (f(l), l) (в унитарном случае она квадратична на овеществленном пространстве). В базисе {e₁, ..., e_n} она приобретает вид

или

и, таким образом, направления Re_i (или Ce_i) суть главные оси q_f.

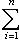
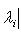
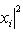
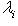Простейшее экстремальное свойство собственных значений выражается следующим фактом.

-1-2-3-4-5-6-7-8-9-10-11-