Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Геометрия квадратичных форм и собственные значения самосопряженных операторов / 1 2 3 4 5 6 7 8 9 10 11
Промежуточные случаи Конусом он называется потому, что заметается своими образующими: прямая, содержащая один вектор из C, целиком лежит в нем. чтобы составить себе представление о базе этого конуса, рассмотрим его пересечение, скажем, с линейным многообразием yn = 1:
Видно, что база является множеством уровня квадратичной формы от n - 1 переменной. Простейший случай получается, когда она положительно определена: тогда это множество уровня есть эллипсоид, в частности, оно ограничено, и наш конус похож на "школьные" трехмерные конусы. Этот случай отвечает сигнатуре (n - 1, 1) или (1, n - 1); при n = 4 пространство (R4, q) есть знаменитое пространство Минковского, которое будет подробно изучено далее. Для дугих сигнатур C устроен заметно сложнее, т. к. его база "уходит на бесконечность". Сечения графика q вертикальными плоскостями, проходящими через образующие C, совпадают с этими образующими. Для любых других плоскостей получаются либо "чаши", либо "купола" - асимптотические направления разделяют эти два случая. Поэтому конус C делит пространство Rn\C на две части, сплошь заметаемые прямыми, вдоль которых q соответственно положительна или отрицательна. Одна из этих областей называется совокупностью внутренних пол конуса C, другая - его внешностью. Геометрический смысл сигнатуры (r, s) грубо, но наглядно можно описать следующей фразой: график формы q по r направлениям уходит вверх, а по s - вниз. Хотя мы работали все время с вещественными квадратичными формами, те же результаты применимы к комплексным эрмитовым формам. Действительно, овеществление Cn есть R2n, и овеществление эрмитовой формы Опишем теперь вкратце и без доказательств два приложения этой теории в механике и топологии. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
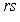
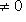 приводят к многомерным гиперболическим параболоидам разных сигнатур. Ключом к их геометрии является снова структура конуса асимптотических направлений C в Rn, т. е. нулевого уровня формы q(y1, ..., yn) = 0.
приводят к многомерным гиперболическим параболоидам разных сигнатур. Ключом к их геометрии является снова структура конуса асимптотических направлений C в Rn, т. е. нулевого уровня формы q(y1, ..., yn) = 0.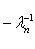
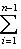
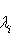
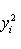
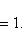
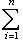
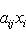
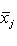
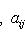
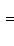
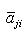 , есть вещественная квадратичная форма. При овеществлении все размерности удваиваются: в частности, комплексная сигнатура (r, s) превращается в вещественную сигнатуру (2r, 2s).
, есть вещественная квадратичная форма. При овеществлении все размерности удваиваются: в частности, комплексная сигнатура (r, s) превращается в вещественную сигнатуру (2r, 2s).