Геометрия пространств со скалярным произведением / Геометрия квадратичных форм и собственные значения самосопряженных операторов / 1 2 3 4 5 6 7 8 9 10 11
б) 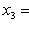 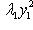  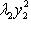 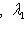 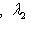 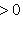 . График является гиперболическим параболоидом. Линии уровня q суть гиперболы, непустые для всех значений x3, так что график уходит и выше, и ниже плоскости x3 = 0; сечения вертикальными плоскостями - по-прежнему параболы. Линия уровня x3 = 0 - это "вырожденная гипербола", сводящаяся к своим асимптотам, двум прямым . График является гиперболическим параболоидом. Линии уровня q суть гиперболы, непустые для всех значений x3, так что график уходит и выше, и ниже плоскости x3 = 0; сечения вертикальными плоскостями - по-прежнему параболы. Линия уровня x3 = 0 - это "вырожденная гипербола", сводящаяся к своим асимптотам, двум прямым 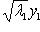 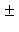 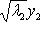 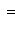 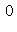 . Эти прямые в R2 называются "асимптотическими направлениями" формы q. Если рассматривать q как (неопределенную) метрику в R2, то асимптотические прямые состоят из всех векторов длины нуль. Асимптотические прямые делят R2 на четыре сектора. Линии уровня q = x3 при x3 > 0 лежат в паре противоположных секторов; когда . Эти прямые в R2 называются "асимптотическими направлениями" формы q. Если рассматривать q как (неопределенную) метрику в R2, то асимптотические прямые состоят из всех векторов длины нуль. Асимптотические прямые делят R2 на четыре сектора. Линии уровня q = x3 при x3 > 0 лежат в паре противоположных секторов; когда 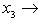 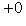 сверху, они "прижимаются" к асимптотам, превращаются в них при x3 = 0 и при x3 < 0, "пройдя насквозь", оказываются в другой паре противоположных секторов. Вертикальные сечения графика плоскостями, проходящими через асимптотические прямые, суть сами эти прямые, "распрямившиеся параболы". сверху, они "прижимаются" к асимптотам, превращаются в них при x3 = 0 и при x3 < 0, "пройдя насквозь", оказываются в другой паре противоположных секторов. Вертикальные сечения графика плоскостями, проходящими через асимптотические прямые, суть сами эти прямые, "распрямившиеся параболы".
Случай - 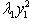 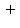  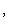 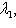 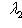 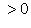 , получается из разобранного заменой знака x3. , получается из разобранного заменой знака x3.
в) 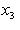 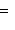 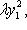 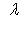 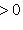 . Поскольку от y2 функция не зависит, сечения графика вертикальными плоскостями y2 = const имеют один и тот же вид: весь график заметается параболой . Поскольку от y2 функция не зависит, сечения графика вертикальными плоскостями y2 = const имеют один и тот же вид: весь график заметается параболой 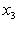 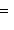 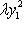 в плоскости (y1, x3) при ее движении вдоль оси y2 и называется параболическим цилиндром. Линии уровня суть пары прямых в плоскости (y1, x3) при ее движении вдоль оси y2 и называется параболическим цилиндром. Линии уровня суть пары прямых 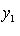 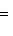 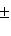 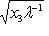 ; при x3 = 0 они склеиваются в одну прямую; весь график лежит над плоскостью x3 = 0. ; при x3 = 0 они склеиваются в одну прямую; весь график лежит над плоскостью x3 = 0.
Случай 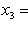 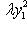 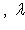 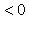 получается "опрокидыванием". получается "опрокидыванием".
г) x3 = 0. Это - плоскость.
-1-2-3-4-5-6-7-8-9-10-11-
|
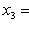
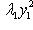

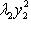
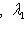
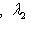
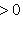 . График является гиперболическим параболоидом. Линии уровня q суть гиперболы, непустые для всех значений x3, так что график уходит и выше, и ниже плоскости x3 = 0; сечения вертикальными плоскостями - по-прежнему параболы. Линия уровня x3 = 0 - это "вырожденная гипербола", сводящаяся к своим асимптотам, двум прямым
. График является гиперболическим параболоидом. Линии уровня q суть гиперболы, непустые для всех значений x3, так что график уходит и выше, и ниже плоскости x3 = 0; сечения вертикальными плоскостями - по-прежнему параболы. Линия уровня x3 = 0 - это "вырожденная гипербола", сводящаяся к своим асимптотам, двум прямым 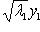
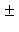
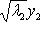
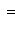
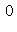 . Эти прямые в R2 называются "асимптотическими направлениями" формы q. Если рассматривать q как (неопределенную) метрику в R2, то асимптотические прямые состоят из всех векторов длины нуль. Асимптотические прямые делят R2 на четыре сектора. Линии уровня q = x3 при x3 > 0 лежат в паре противоположных секторов; когда
. Эти прямые в R2 называются "асимптотическими направлениями" формы q. Если рассматривать q как (неопределенную) метрику в R2, то асимптотические прямые состоят из всех векторов длины нуль. Асимптотические прямые делят R2 на четыре сектора. Линии уровня q = x3 при x3 > 0 лежат в паре противоположных секторов; когда 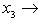
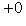 сверху, они "прижимаются" к асимптотам, превращаются в них при x3 = 0 и при x3 < 0, "пройдя насквозь", оказываются в другой паре противоположных секторов. Вертикальные сечения графика плоскостями, проходящими через асимптотические прямые, суть сами эти прямые, "распрямившиеся параболы".
сверху, они "прижимаются" к асимптотам, превращаются в них при x3 = 0 и при x3 < 0, "пройдя насквозь", оказываются в другой паре противоположных секторов. Вертикальные сечения графика плоскостями, проходящими через асимптотические прямые, суть сами эти прямые, "распрямившиеся параболы".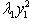
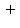

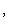
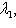
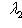
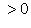 , получается из разобранного заменой знака x3.
, получается из разобранного заменой знака x3.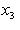
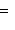
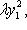
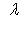
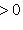 . Поскольку от y2 функция не зависит, сечения графика вертикальными плоскостями y2 = const имеют один и тот же вид: весь график заметается параболой
. Поскольку от y2 функция не зависит, сечения графика вертикальными плоскостями y2 = const имеют один и тот же вид: весь график заметается параболой 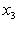
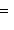
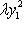 в плоскости (y1, x3) при ее движении вдоль оси y2 и называется параболическим цилиндром. Линии уровня суть пары прямых
в плоскости (y1, x3) при ее движении вдоль оси y2 и называется параболическим цилиндром. Линии уровня суть пары прямых 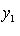
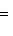
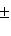
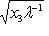 ; при x3 = 0 они склеиваются в одну прямую; весь график лежит над плоскостью x3 = 0.
; при x3 = 0 они склеиваются в одну прямую; весь график лежит над плоскостью x3 = 0.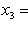
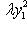
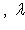
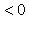 получается "опрокидыванием".
получается "опрокидыванием".