Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Евклидовы пространства / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
4. Следствие. Евклидова длина вектора | l | является нормой на L в смысле определения в п. 4, а функция d(l, m) = | l - m | - метрикой в смысле определения п. 1. Доказательство. Остается проверить только, что | al | = | a | | l | для всех
5. Углы и расстояния. Пусть
Поэтому существует единственный угол
Он называется углом между векторами l1, l2. Поскольку скалярное произведение симметрично, это "неориентированный угол", чем и объясняется интервал его значений. В соответствии со школьной геометрией угол между ортогональными векторами равен -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
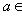
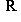 , но
, но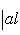
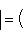
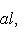
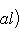
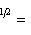
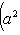
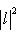
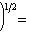
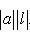
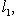
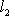
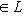 - ненулевые векторы. В силу предложения п. 2
- ненулевые векторы. В силу предложения п. 2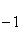
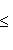

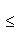
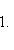
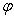
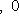
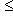

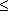
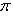 , для которого
, для которого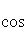
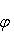
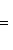
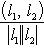

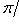
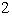 . Можно систематически развивать евклидову геометрию на основе данных определений длины угла и убедиться, что в размерностях два и три она совпадает с классической.
. Можно систематически развивать евклидову геометрию на основе данных определений длины угла и убедиться, что в размерностях два и три она совпадает с классической.