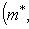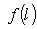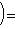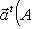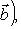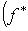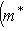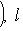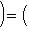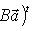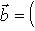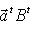Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Двойственность / 1 2 3 4 5
3. Двойственное, или сопряженное отображение. Пусть (f*(m*), l) = (m*, f(l)) для любых векторов а) Единственность f*. Пусть б) Существование f*. Фиксируем
следует из линейности (m*, f(l)), по m*. Значит f* - линейное отображение. Пусть в L, M выбраны некоторые базисы, а в L*, M* - двойственные базисы. Пусть f в этих базисах представлено матрицей A. Утверждаем, что f* в двойственных базисах представлено транспонированной матрицей At. В самом деле, пусть B - матрица f*. Согласно определениям и п. 2 имеем, обозначив вектор-столбцы координат m*, l через
Из ассоциативности умножения матриц и единственности f* следует, что A = Bt, т. е. B = At. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
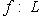
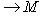 - линейное отображение линейных пространств. Покажем, что существует единственное линейное отображение
- линейное отображение линейных пространств. Покажем, что существует единственное линейное отображение 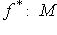
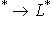 , которое удовлетворяет условию
, которое удовлетворяет условию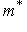
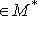 ,
, 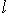
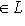 .
.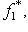
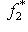 - два таких отображения. Тогда
- два таких отображения. Тогда 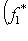
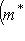
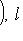
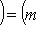
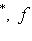
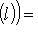
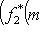
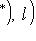 для всех
для всех 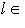
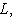 , откуда следует что
, откуда следует что 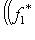
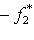
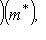
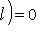 . Фиксируем m* и будем менять l. Тогда элемент
. Фиксируем m* и будем менять l. Тогда элемент 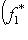
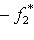
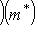
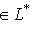 как линейный функционал на L принимает только нулевые значения и, значит, равен нулю. Поэтому
как линейный функционал на L принимает только нулевые значения и, значит, равен нулю. Поэтому 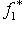
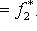
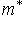
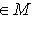 и рассмотрим выражение (m*, f(l)) как функцию на L. В силу линейности f и билинейности (,) эта функция линейна. Значит, она принадлежит L*. Обозначим ее через f*(m*). Равенства
и рассмотрим выражение (m*, f(l)) как функцию на L. В силу линейности f и билинейности (,) эта функция линейна. Значит, она принадлежит L*. Обозначим ее через f*(m*). Равенства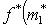
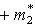
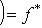
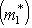
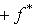
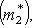
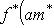
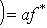
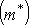
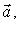
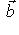 ,
,